文 | jemand
编辑 | 贰沐 子鱼
声学超构材料与拓扑绝缘体模拟
上两篇[当声学遇见凝聚态(一)& 当声学遇见凝聚态(二)]的内容和声学有什么关系呢?这里就要提到在声学,尤其是物理声学中非常热门的一类课题,就是声学超构材料。简而言之,声学超构材料通过对材料结构的刻意设计使得声波在通过这类材料的时候被有目的地控制、调制, 从而获得在常规材料中不容易获得的宏观材料参数(比如有可能调出负的弹性模量和负的折射率)或波调控效应。比如香港科大的沈平教授等人利用声学谐振腔设计出来的结构可以将材料的吸声频率控制在一个特定的区间[2];南京大学的程建春教授等人在2009年设计出的声二极管可以对声波进行像电流一样的整流操作[3]等等。还有其他的方向,比如声聚焦,声成像,声镊等都可以看到超材料参与其中。而本文要提到的是超材料的一类比较新的应用方向,就是对凝聚态现象的模拟,其中以拓扑材料为主。
其实说起来原理也很简单,材料中的电子波函数遵守的定态薛定谔方程和声波遵守的波动方程都是二阶线性偏微分方程,从数学上说两者确实有相似之处。那么既然我们可以计算电子在周期势场中的能带,那对于声波我们也可以定义类似的东西。这个时候用来作为‘周期势场’的就是提前设计好的超构材料。
以 Zhaoju Yang 等人在2015年发表的一篇文章[1]为例。在文中,作者设计了一个周期性的结构,如图8。灰色的圆柱以三角格子的形式周期排布,每一个圆柱浸没于一定宽度的流体中,而圆柱和周围流体又一起浸没与外界流体中并与之隔离。圆柱以一定角速度进行旋转,并通过液体粘性带动其周围液体旋转。

图8 二维声学拓扑绝缘体结构示意[1]
声波在其中传播服从的波动方程可以被写得非常像带有电磁势的定态薛定谔方程:

而最后计算得出的能谱也和之前提到的真实的拓扑绝缘体非常类似:

图9 声学拓扑绝缘体能带示意[1]
下图是计算得出的声波边界态在边缘传播的声压分布,可以注意到声波沿边缘单向传播,而且向内部衰减,这符合边界态的特点。
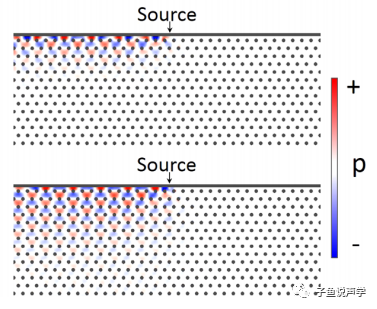
图10 声学拓扑绝缘体能带示意[1]
以上工作仅限于计算,真正的实验实现是在2019年由南京大学的程建春教授课题组做出的。他们设计的材料结构和上面的理论工作类似,如下图。每一个晶格节点由一个电机带动的旋转的圆盘构成,圆盘之间由波导管连接,整个结构符合晶体的紧束缚模型。声波由某一点馈入进行传播。
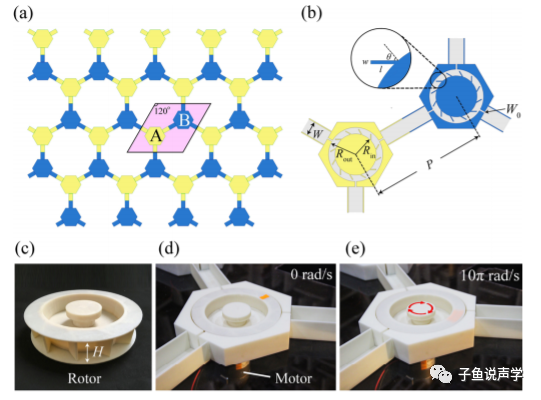
图11 声学拓扑绝缘体实验结构示意[4]
实验结果如下图,也是和实际的拓扑绝缘体的能带很像。红蓝两条线表示上下两个边界态。图13中左图和右图给出了上下两个边界态的声压测量结果,中间是拓扑平庸的体态。

图12 声学拓扑绝缘体实验结构示意[4]
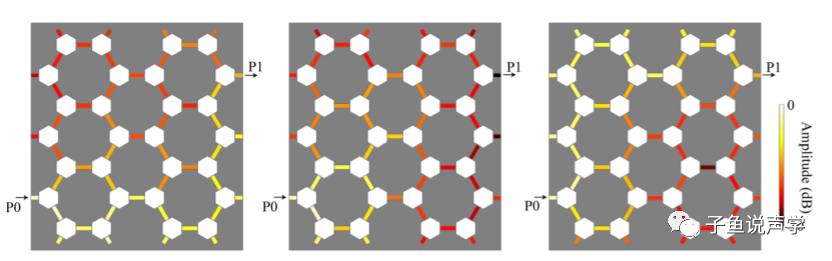
图13 边界态声压测量结果[4]
其实这种模拟也不仅限于拓扑绝缘体,凡凝聚态界比较有名的结构大概都已经被拿来尝试过了,外尔半金属,马拉约那零能模等等,在此就不多介绍了。由于这类超构材料的这种和材料周期性相关的调制功能,有时也会被称为声子晶体 (phononic crystal)。这样看来其实还蛮贴切的。

作者:jemand,南京大学物理学本科毕业,亚琛工业大学物理学硕士在读,大概以后是会去做声学相关的工作,以上。
参考
[1] Z. Yang, F. Gao, X. Shi, X. Lin, Z. Gao, Y. Chong, and B. Zhang, Phys. Rev. Lett. 114, 114301 (2015).
[2] M. Yang, S. Chen, C. Fu, and P. Sheng, Materials Horizons, 4(4), 673-680 (2017).
[3] B. Liang, B. Yuan, and J. Cheng, Phys. Rev. Lett. 103, 104301 (2009).
[4] Y. Ding, Y. Peng, Y. Zhu, X. Fan, J. Yang, B. Liang, X. Zhu, X. Wan, and J. Cheng, Phys. Rev. Lett. 122, 014302 (2019).
封面来源:wikipedia


 业务咨询
业务咨询